Численное построение аттракторов
полудинамических систем
А. А. Корнев.
В данной работе для полудинамических систем (ПДС), обладающих компактным аттрактором, хорошей
функцией Ляпунова, конечным числом изолированных, возможно негиперболических, неподвижных точек,
явно решается задача численного нахождения аттрактора с требуемой точностью.
В работе применяются новые результаты о структуре неустойчивых многообразий в окрестности негиперболической точки.
Введение
При исследовании различных нестационарных физических явлений возникает задача описания всех состояний систеым,
которые могут наблюдаться по прошествии достаточно большого
промежутка времени. Особенный интерес представляет
минимальное множество состояний, равномерно притягивающих с
течением времении все траектории, выходящие из некоторого
подмножества начальных данных.
К концу 40-х годов, в основном, была построена теория предельных
множеств для ПДС в локально компактных пространствах.
Первые результаты для ПДС, действующих в нелокально компактных пространствах, были получены
в работах Дж. Хейла и его коллег [1] при
исследовании ОДУ с запаздывающим аргументом. Приблизительно в это
же время О.А.Ладыженская [2] для двумерных уравнений
Навье-Стокса построила множество M, равномерно
притягивающее произвольное ограниченное подмножество B исходного
пространства H. Была доказана минимальность данного множества среди
всех, обладающих этим свойством, строгая инвариантность
относительно разрешающего оператора задачи. Среди всех строго
инвариантных подмножеств пространства M является максимальным. Само M
компактно и связно. На нем исходная
полугруппа S(t,h) продолжается до непрерывной группы. Каждая
полная траектория из M определяется ее ортопроекцией на некоторое фиксированное конечномерное подпространство.
Построенное множество было названо минимальным глобальным
B-аттрактором ПДС. В настоящий момент M обычно называют [3] глобальным аттрактором.
Теория аттракторов эволюционных уравнений (теория глобальной
устойчивости) развивалась в работах А.В.Бабина, М.И.Вишика [4], О.А.Ладыженской [5], Р.Темама [3] и их последователей. Полученные к настоящему
моменту результаты охватывают весьма широкий класс задач математической физики.
Свойство компактности глобального аттрактора позволяет аппроксимировать его конечной
ε-сетью с любой точностью. Имеется покрайней мере два подхода к построению такой
аппроксимации. Первый подход основан на свойстве равномерного притяжения к аттрактору [6] произвольного ограниченного
подмножества, второй - на возможности продолжить на M исходную ПДС до непрерывной группы [7]. В данной работе мы
остановимся на первом подходе. Его суть заключается в численной реализации известной формулы:
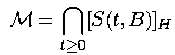
Общая динамика на Аттракторе Лоренца (приближение Лоренца для уравнений Навье-Стокса)
 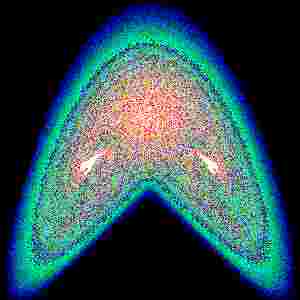 
Несмотря на наличие соответствующих алгоритмов (отметим существенную нетривиальность доказательства их сходимости) и
огромное число картинок типа "странные аттракторы", сколько-нибудь строгие численные расчеты практически отсутсутвуют.
В первую очередь это связано с огромной вычислительной трудоемкостью данных задач - при построении
ε-сети, например с ε = 0.01, аппроксимирующей аттрактор, нам потребуется
решить рассматриваемое нестационарное уравнение на некотором
отрезке [0,T] с порядка (Cε)-N различными
начальними данными. При этом C много меньше 1, а N много больше 100 совпадает
с размерностью подпространства функций, на котором ищется решение, в методе сеток для урчп - с количеством узлов сеток.
При этом отсутствует соответствующий математический аппарат обоснования "достоверности" полученных
картинок, который, в некоторых случаях, можно было бы компенсировать дополнительными затратами.
В связи с этим, например, для классических задач Чафе-Инфанта [8] и уравнений Лоренца
отсутствуют численные эксперименты по построению аттрактора, хотя описанию его структуры уделено много места и она
продолжает уточняться [12].
В данной работе рассматривается иная формулировка [10] проблемы аппроксимации аттрактора с требуемой точностью. С одной
стороны, она эквивалентна в некотором смысле [11] исходной, с другой - позволяет явно решить рассматриваемую задачу для некоторого класса ПДС.
Суть этого подхода заключается в использовании свойств функции скорости притяжения к аттрактору.
Отметим, что существование функции скорости притяжения к аттрактору
естественно следует из определения глобального аттрактора.
Полный текст - в формате pdf, 160 Кбайт
СПИСОК ЛИТЕРАТУРЫ
- Hale J.K., La Salle J.P., Slemrod M., Theory of
a general class of dissipative process // J. Math. Anal. Appl.
1972. Vol. 39. p. 177-191.
- Ладыженская О.А. О динамической системе, порождаемой
уравнениями Навье-Стокса // Зап. научн. сем. ЛОМИ. 1972. т. 27.
с. 97-114.
- Temam R. Infinite dimensional system in
mechanics and physics. New York: Springer-Verlag, 1998.
- БабинА.В., Вишик М.И. Аттракторы
эволюционных уравнений. М.: Наука, 1989.
- Ладыженская О.А. О нахождении глобальных
минимальных аттракторов для уравнений Навье-Стокса и
некоторых других уравнений в частных производных // Усп. Матем. Наук. 1987. т. 42.
N. 6. с. 25-60.
- Костин И.Н., Об одном способе аппроксимации аттракторов //
Зап. научн. сем. ЛОМИ. 1991. т. 188. с. 87-104.
- Foias C., Jolly M.S., Kukavica I., Localization
of attractors by their analytic properties // Nonlinearity. 9. 1996.
p. 1565-1581.
- M. Hirsch, C. Pugh and M. Shub. Invariant
manifolds. Lectures notes in Math. vol. 583. Springer. Berlin.
1977.
- Kostin I.N. Rate of attraction
to a non-hyperbolic attractor. Asymptotic Analysis 1998. 16. p. 203-222.
- Корнев А.А. К вопросу об аппроксимации полудинамических систем //
Вестник МГУ. сер. "Матем. Механика." 2000. N 3. с. 24-28.
- Корнев А.А. Об одном критерии аппроксимации
аттракторов полудинамических систем // 1999. ДАН. т. 369, N 5.
- Нитецки З. Введение в дифференциальную динамику. М.: Мир. 1975.
|